Introduction
Let's Begin with Some Important Background Information. Let me ask you a question: do you use Google Search or Google Maps? OR Do you use social networking sites?
If you answered "yes" to any of the questions, you've most likely used graphs without even realizing it!
Because of their incredible capabilities, these data structures piqued our interest. They are so powerful that you can't even imagine how many different real-world applications they can have. Let's get started!
Application Of Graphs
Graphs are used in a wide range of industries and fields :
1. Graphs are used by GPS systems and Google Maps to determine the shortest route from one location to another.
2. Graphs are used in social networks to represent user connections.
3. Graphs are used by the Google Search algorithm to assess the relevance of search results.
4. Operations Research is a field that employs graphs to determine the best path to take in order to decrease the cost of transportation and the delivery of goods and services.
5. Even in chemistry, graphs are used to represent molecules!
Let's look at a real-world example of a graph - a graph of users - META (Facebook).
Although Facebook users are not required to understand graph theory, once you create your profile, Facebook uses graphs to model relationships between nodes.
We can use graph algorithms to recommend friends, calculate the number of mutual friends, and so on.
Assume you have Facebook friends X, Y, and Z. And you share one common friend with all three.
Now, Facebook monitors connections and suggests that your friends connect with each other based on your connection with them.
And you'd be shown as a single mutual friend to all three of them, which is the idea behind the mutual friends and friends suggestions system.
The following are the fundamental graph terminologies in data structures:
- One of the two primary units used to construct graphs is the edge. Each edge has two ends that are connected to vertices.
- They are adjacent if two vertices are endpoints of the same edge.
- The outgoing edges of a vertex are directed edges that point to the origin.
- Incoming edges of a vertex are directed edges that point to the vertex's destination.
- The degree of a vertex in a graph is the total number of edges that occur to it.
- In a directed graph, the out-degree of a vertex is the total number of outgoing edges, whereas the in-degree is the total number of incoming edges.
- A vertex with an in-degree of zero is called a source vertex, and one with an out-degree of zero is called a sink vertex.
- An isolated vertex is a zero-degree vertex that is not the endpoint of an edge.
- A path is an alternating set of vertices and edges, with each vertex connected by an edge.
- A cycle is defined as a path that begins and ends at the same vertex.
- A simple path is one that has unique vertices.
- A graph is strongly connected if it contains a directed path from x to y and a directed path from y to x for each pair of vertices x, y.
- If all of a directed graph's directed edges are replaced with undirected edges, the result is a connected graph. The vertices of a weakly linked graph have at least one out-degree or in-degree.
- A tree is a part of a connected forest. A rooted tree, also known as a free tree, is the tree's primary form.
- A spanning tree is a spanning subgraph that is also a tree.
- A connected component is the most connected subgraph of an unconnected graph.
- A bridge, which is a removal edge, would sever the graph.
- Forest is a graph that lacks a cycle.
Representation Of Graphs
Any representation should be able to store the nodes of a graph as well as their connections. And this can be accomplished in a variety of ways, but the most common way to represent a graph is,
- Adjacency List - Label the nodes according to their neighbors.
- Adjacency Matrix - Aij = 1 if I and j have an edge, 0 otherwise.
Adjacency List:
In this method of graph representation, we store the nodes as well as a list of their neighbors. Essentially, we keep a list of all the does, as well as the list of nodes to which each node is connected. Consider the nodes I've drawn below.
So, first, we save the nodes in the graph.
Then we take a glance at the connections between each of the nodes we saved. Starting with 0, we can see that it is linked to both 1 and 2. So we'll keep that alongside node 0. Following that, 1 is linked to all 0s, 2s, and 3s. 2 is linked to both 0 and 4, 3 is linked to only 1, and 4 is linked to only 2. As a result, this data is saved as shown below.
And the information about each node's connections is saved in separate linked lists, as depicted in the figure above. And each node is considered as a pointer saved in an array pointing to the beginning of each linked list.
In this case, we would use an array of length 5 with the first index storing a pointer to the head of node 0's adjacency linked list.
This represented the adjacency list, which is one of the most commonly used representation methods. The adjacency matrix follows.
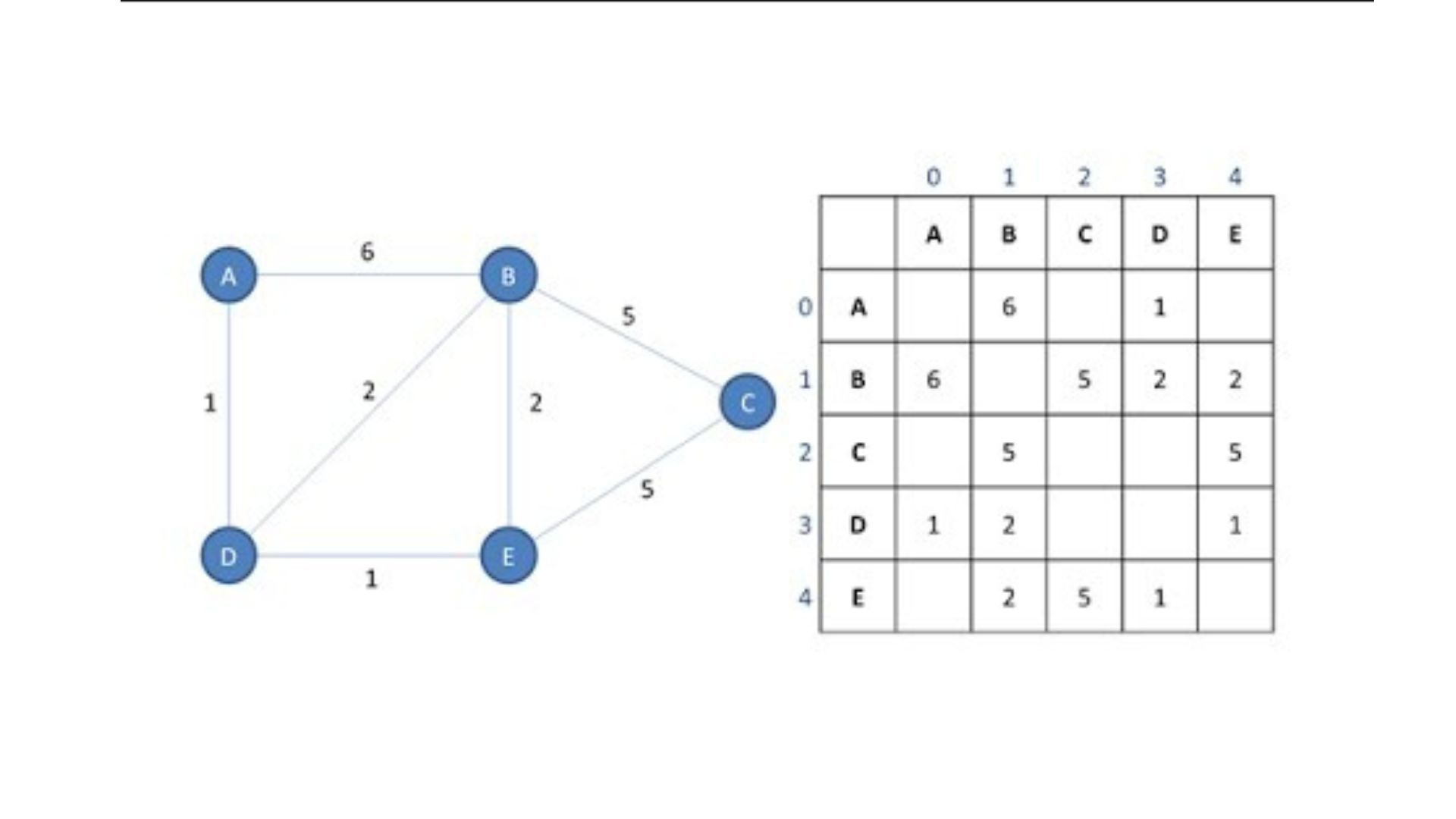
Adjacency matrix
An adjacency matrix is another technique of graph representation in which we represent our graph as a matrix with cells filled with 0 or 1.
If we call the cell at the intersection of the ith row and the jth column Aij, it will be filled with a 1 if we have an edge between nodes I and j, otherwise, it will be filled with a 0.
GRAPH:
REPRESENTATION:
COSTS:
