Advanced Algorithms and Problem Solving Techniques
How To Start Competitive Programming - A Complete Guide
A Quick Guide to Breadth-First Search
Depth First Search (DFS) with Explanation and Code
Difference Between BFS and DFS (with code and diagrams)
How to Perform Level Order Traversal?
A Quick Guide to Backtracking Algorithm
Solving N Queens Problem using Backtracking
Quick Guide to Divide and Conquer Algorithm
Longest Increasing Subsequence Problem
Quick Note - Greedy Programming v/s Dynamic Programming
Coin Change Problem: DP and Recursion Approach
A Definitive Guide to Knapsack Problem
How to Solve Subset Sum Problem?
Understanding Huffman Coding in detail
Understand the working of KMP Algorithm
Longest Common Substring Problem
Longest Common Subsequence problem: solved
A Quick Guide to Manacher's Algorithm
Learning About Bipartite Graphs
Graph Coloring Problem: Explained
Detect Cycle in Direct Graph
Directed Acyclic Graph: Representation
Prim's Algorithm: Explanation, Code, and Applications
Working of Kruskal's Algorithm
Prims and Kruskal algorithm for Maximum Spanning Tree
Bellman Ford Algorithm in detail with code
Floyd-Warshall Algorithm and its Implementation
Understand Travelling Salesman Problem
Branch And Bound Algorithm: Explained
How to Evaluate Postfix Expression
Introduction to Round-Robin Scheduling
Disjoint set (Union find Algorithm)
State Space Reduction in Algorithms
Apriori Algorithm
What is A* Search Algorithm?
Introduction
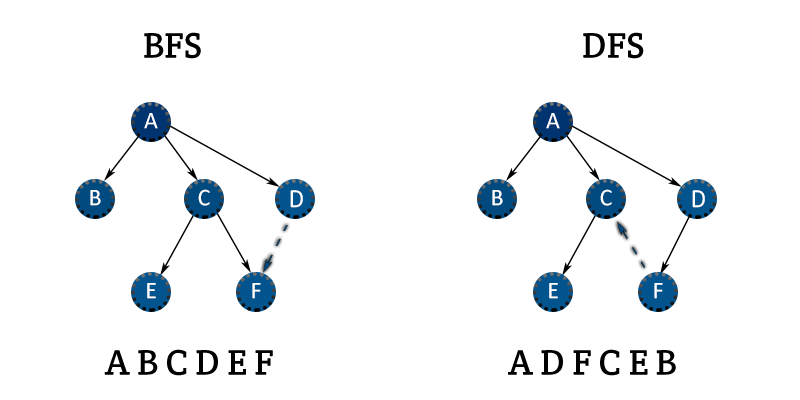
Two significant search algorithms are Breadth-First Search (BFS) and Depth First Search (DFS). When conducting a search, Breadth-First Search begins at the top node and moves down through the lower tiers to the root node, whereas Depth-First Search begins at the top node and follows the path until it reaches the path's end node. During the search, both algorithms go through every node. To carry out the traversing process for the two algorithms, different codes are written.
Traversal Technique
BFS - BFS grows the tree level by level
DFS - DFS grows it sub-tree by sub-tree.
Comparison Table
BFS | DFS |
BFS stands for Breadth-First Search. | DFS stands for Depth First Search. |
In order to determine the shortest path, BFS traverses all of its nodes that are connected to the individual nodes, starting with the first or root node. After reading the example below, you will clearly understand how it functions. | DFS uses a depth-based methodology and traverses every node connected to the relevant node in its entirety. After reading the example below, you will clearly understand how it functions. |
It is carried out utilizing the First In, First Out (FIFO) principle (FIFO) whilst using the Queue data structure. | Utilizing the Last In First Out (LIFO) method and using the Stack data structure. |
Multiple traversals of a node result in its removal from the queue. | When there are no additional nodes to be visited, the visited nodes are removed from the stack. |
Compared to Depth First Search, it is slower. | Compared to the Breadth-First Search algorithm, it is quicker. |
Consumes more memory than DFS where stack occupies less memory. | Memory allocation is low compared to BFS. |
The applications of DFS include the inspection of two edge connected graphs, strongly connected graphs, acyclic graphs, and topological order. | BFS can be useful in finding whether the graph has connected components or not. And also it can be used in detecting a bipartite graph. |
Code for BFS
#include <iostream> |
Code for DFS
#include <iostream> |
Hope this gave you a clear understanding of DFS and BFS and key differences between them.
