A Definitive Guide to Knapsack Problem

The Knapsack algorithm is one of the computerisation models, most used when seeking to solve optimisation problems. It is used in the organization planning, resource management, and allocation, quotas and standards setting, and storing and transportation. Despite its basic look the knapsack problem is one of the most popular examples of combinatorial optimization with definite subtleties.

This blog provides a comprehensive coincidence of the knapsack problem, different types of problems, approaches to solving the problem, its applications, and an exercise in the form of a list of frequently asked questions to ensure better understanding.

What is the Knapsack Problem?

The knapsack problem is named after the case where it is up to a hiker on which items should be taken to the knapsack to get maximum value yet the knapsack has limited capacity on the weight that it can hold. In simpler terminology, it means choosing a number of objects each of which has its own weight and value, so that the sum of their values is a maximum without exceeding the total weight that has been allowed.

Formal Definition

The, there deletes for instance a binary variable r indicating whether an item is included in an item set (r= 1) or not (r= 0).

Types of Knapsack Problems

✅0/1 Knapsack Problem

In this case for each item, it can either be taken or it can not be taken to the knapsack. This binary option results into 2^n , possible combination of n items; this makes it quite slow especially when dealing with large number of dataset.

✅Fractional Knapsack Problem

Here portions can be made and one can be able to take portion of the item as a way of portioning the stuff. This problem is to be solved in polynomial time by greedy algorithm, thus it is comparatively easier than 0/1 version.

✅Unbounded Knapsack Problem

In this variant it is not limited in the number of selections of any item but one has to ensure that the total weight does not exceed ‘W’.

Solving the Knapsack Problem

✅Dynamic Programming Approach (0/1 Knapsack)

The dynamic programming (DP) solution involves constructing a 2D table where:

1. Rows represent items
2. Each column depicts weight from 0 to W as far as the weights are concerned.

Recurrence Relation:

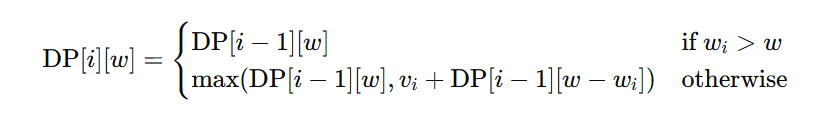
Steps:

1. Begin constructing a DP table with row size n+1 which will contain the item quantities and with a column size W+1 containing the weights.
2. Fill the table row by row.
3. The value present at DP[n][W] provides the maximum possible value for the topology.

Time Complexity: O(nW)

✅Greedy Algorithm (Fractional Knapsack Algorithm)

Steps:

1. Determine the value-to-weight ratio i.e vi/wi for each of the items.
2. Arrange items in such away that; Those with the highest ratio will be ranked lower while those with the least ratio will be ranked higher.
3. Choose items as much as possible until the knapsack is capacity is reached.

Time Complexity: O(nlog⁡n) for sorting

✅Backtracking and Branch-and-Bound

For optimization or larger problems:

• Backtracking: Enumerates over all possibilities and removes all combinations that don’t work.
• Branch-and-Bound: Delves into combinations systematically and employs bounds so as to rule out certain paths from revealing potential excellent solutions.

Time Complexity: Exponential in the worst case.

Applications of Knapsack Algorithm

1. Resource Allocation: Choosing what is to be done with limited resources such as communication bandwidth or disk space.
2. Investment Planning: Choosing the right balanced portfolio given a target rate of return within the given investment funds.
3. Supply Chain Management: Stressing the best way of loading the cargo in order to achieve the maximum profit between the maximum allowable weights.
4. Cryptography: The knapsack problems are close with the subset-sum problem of the public-key cryptosystem.
5. Video Game Design: Limited parts stock on the basis of weight or value.

Knapsack Problem Variants

✅Multi-Knapsack Problem

There are many knapsacks, requiring to divide items to maximize total value.

✅Knapsack with Additional Constraints

The model considered some constraints that are not applicable in the basic knapsack portion of the genetic algorithm. Restrictions like, the total number of products that should be produced say, three products, or how one product depends on another in terms of production.

✅Subset-Sum Problem

A basic form of the problem where vi=wi, concerning the attainment of a particular total weight.

Example Problem

Problem: You have the following items:

• Item 1: Weight = 1, Value = 6
• Item 2: Weight = 2, Value = 10
• Item 3: Weight = 3, Value = 12

Knapsack Capacity: W=5W = 5W=5

Solution Using Dynamic Programming:

1. Construct a DP table.
2. Compute values iteratively.
3. For the purpose of this assessment, the attainable highest score is 22 which is attained when items 2 and 3 are included in the assessment score.

Conclusion

Hence the knapsack problem is another redefined optimization problem in computer science field. Due to its versatility and demand, and contentious characteristics it is respected and appreciated by the researchers as well as practitioners. That is why knowing its types and solving approaches will help to address a large number of optimization problems and practical tasks.

It does not matter if you are a student researching algorithm design or a professional who is trying to optimize resource usage – knowing the knapsack algorithm is essential.