Mastering Fundamentals: C++ and Data Structures

Stack using Linked List in C++

Board Infinity
Board Infinity
Stack using Linked List in C++

    Header in C++

    C++ Pointers

    Displaying A to Z characters using a loop: C++ Program

    Working of Jump Statements in C++

    Inline Functions in C++

    Understanding Substr() Function in C++

    Constructor vs Destructor in C++

    Understanding Copy Constructor in C++

    Becoming Friends with Friend Function in C++

    How File Handling Works in C++

    A Detailed Overview of Macros in C++

    List in C++

    A Set Data Structure (STL) In C++

    A Quick Guide to Circular Linked List in C++

    Stack using Linked List in C++

    How to Sort a Vector in C++

    What are Priority Queues in C++?

    Guide To 5 Data Structures In C++

Introduction

A data structure called a stack uses the Last-In-First-Out (LIFO) principle. The data or element at the top of the stack, which was saved last, will be accessed first. Additionally, the top is where both insertion and deletion happen. To use the linked list to prepare a stack we consider:-

  • If there are additional members to add, the array's size cannot be increased once it is created.
  • We will squander a lot of memory space if we design a really huge array.
  • In order to address this, let's attempt to create a stack using a linked list, where we will dynamically grow the stack's size as necessary.
  • Using this as the foundation of our Node's structure we will discuss the implementation

Implementation using Linked List

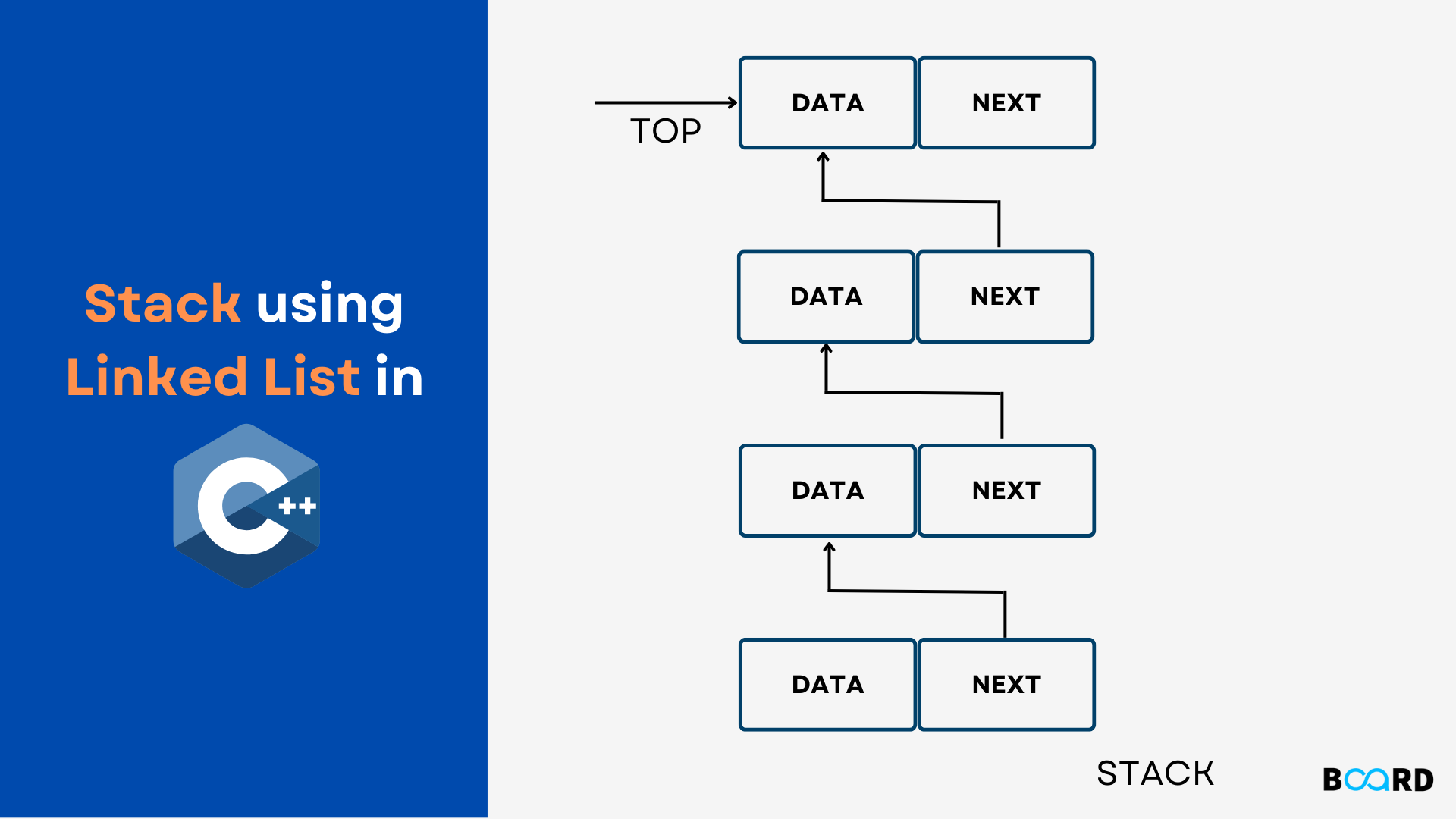
Given that we utilize a head pointer to keep track of the beginning of our linked list, we can simply refer to the head pointer as top when creating a stack using a linked list to make it more related to a stack.

  • Push (insert element in stack)
  1. Similar to putting a node at the beginning of the linked list, the push operation would be.
    Therefore, the top pointer will initially be NULL when the Stack (Linked List) is empty. Let's say we need to add the numbers 1, 2, and 3 to the stack.
  2. So, using the new operator, we will first build a new Node and return its address as a temporary pointer ptr.
  3. Then, we will make the link section of the node equal to the top by setting ptr->link=top and inserting the value 1 in the data part of the node using ptr->data = value.
  4. Finally, we will set top = ptr to refer to the newly generated node, which will serve as both the top of our stack and the beginning of the linked list.

5.   Similarly, if we put the values 2 and 3 into the stack, a linked list of three nodes will result, with the top pointer referring to the node containing the value 3.

  • Pop (delete element from stack)
  1. The pop operation is comparable to removing a beginning node from a linked list. Therefore, we shall compare a temporary pointer (ptr) to the top pointer.
  2. The top pointer will then be moved to the subsequent node, top = top->link.
  3. Using the delete operator and pointer ptr, or delete, we will finally delete the node (ptr)
  4. Our stack will appear something like this after we pop once:
  • isEmpty (stack empty or no checker)

Simply checking whether top == NULL, which denotes that the stack is empty, will tell us whether the stack is empty or not.

C++ Implementation

#include <iostream>
using namespace std;

//Structure of the Node
struct Node
{
int data;

Node *link;
};

Node *top = NULL;


bool isempty()
{
 if(top == NULL)
 return true; else
 return false;
}


void push (int value)
{
  Node *ptr = new Node();
  ptr->data = value;
  ptr->link = top;
  top = ptr;
}

void pop ( )
{
 if ( isempty() )
  cout<<"Stack is Empty";
 else
 {
  Node *ptr = top;
  top = top -> link;
  delete(ptr);
 }
}


void showTop()
{
 if ( isempty() )
  cout<<"Stack is Empty";
 else
  cout<<"Element at top is : "<< top->data;
}

void displayStack()
{
 if ( isempty() )
  cout<<"Stack is Empty";
 else
 {
  Node *temp=top;
  while(temp!=NULL)
  {   cout<<temp->data<<" ";
   temp=temp->link;
  }
  cout<<"\n";
 }
 }

// Main function
int main()
{

 int choice, flag=1, value;

 //Menu Driven Program using Switch
 while( flag == 1)
 {
 cout<<"\n1.Push 2.Pop 3.showTop 4.displayStack 5.exit\n";
 cin>>choice;
 switch (choice)
 {
 case 1: cout<<"Enter Value:\n";
         cin>>value;
         push(value);
         break;
 case 2: pop();
         break;
 case 3: showTop();
         break;
 case 4: displayStack();
         break;
 case 5: flag = 0;
         break;
 }
 }
return 0;
}

Time Complexity - Each operation is O(1)

write your code here: Coding Playground