Time Complexity of Sorting Algorithms

Sorting Algorithms Time complexity shows how a sorting techniques performs in relation to the number of operations within the correlated input quantity. This measure is important because it’s used to evaluate the best sorting algorithm across all sorting techniques depending on resource demands and quantity of data. Optimality of the time complexity reduces the amount of computation required reducing time where large sets of data are involved.

Understanding Time Complexity

In computer science as a field, time complexities can be used to compare the efficiency of an algorithm especially as it relates to sorting, managing, and organizing data in an efficient manner.

Types of Time Complexity: Best, Average, and Worst-Case Scenarios

There are three types of Time Complexity: the Best, the Average, and the Worst. Let’s understand each of them in detail.

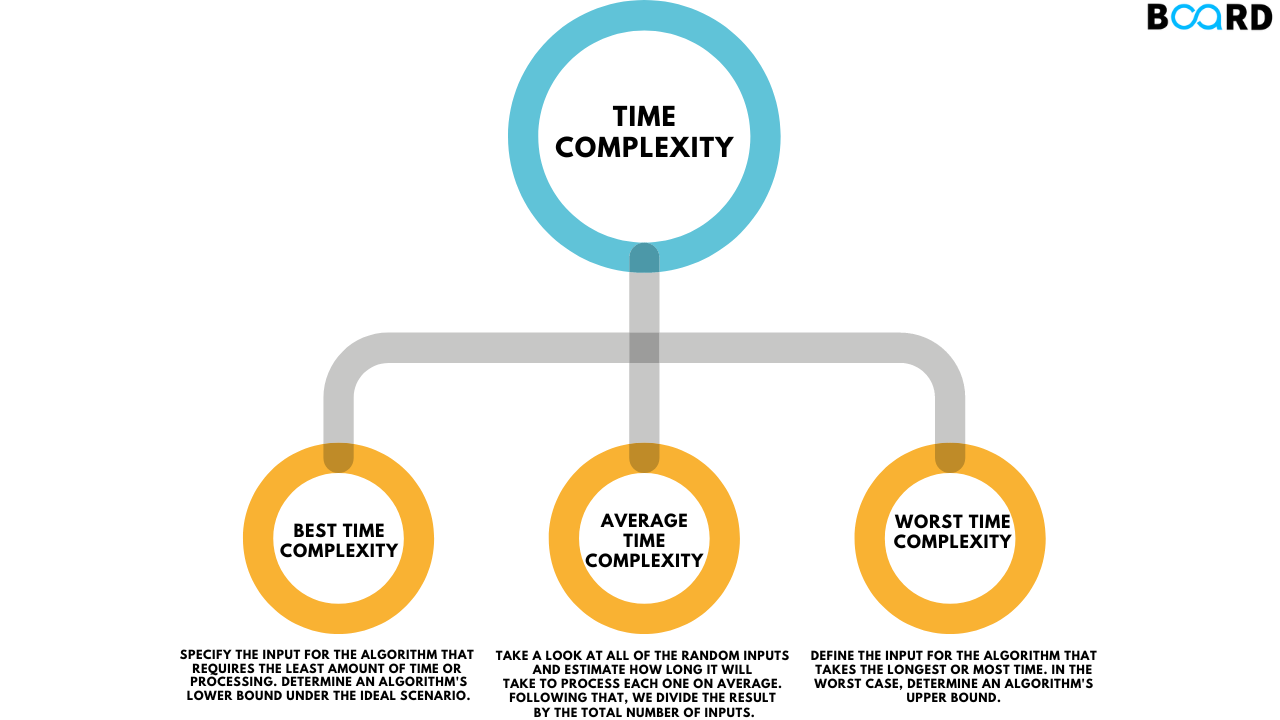
✅Best-Case Time Complexity: The least amount of time an algorithm can possibly require in order to run, they are usually applied on input data that is already sorted or in an exemplary form for the algorithm.

✅Average-Case Time Complexity: The time for which an algorithm takes to complete its process with the input it is most likely to receive most often. This measure offers a way of approximating performance under conditions’, Saying this helps us approximate actual performance situations.

✅Worst-Case Time Complexity: The amount of time that an algorithm might take to solve a problem, this is normally given when the input is worst case. Understanding this enables the determination of the amount of resources to allocate to the algorithm so that it will be equipped to deal with the biggest expected input.

Common Sorting Algorithms Time Complexity

Here in this section, we aim to introduce six commonly–used sorting algorithms.  

✅Bubble Sort

Bubble Sort is also known as sinking sort, as it works by repeatedly stepping through the list comparing the adjacent items, and swapping them if they are in the wrong order. This process is carried out until a list has been sorted.

• Best Case: 𝑂(𝑛) - It is given that the input array is sorted.
• Worst Case: O(n2) — When the array is in descending order.
• Time Complexity Analysis: Bubble Sort is deemed unsuitable for large datasets as it involves the comparison of pairs of elements, successive passes, and even some elements that have been sorted. It’s usually summarized as being for pencil-and-paper sort algorithms or small to mostly sorted lists.

✅Selection Sort

Selection Sort functions in the way that the routine chooses the smallest (or largest) item from the segment of the unsorted array and swaps it with the very first element in the unsorted part of the list and only the sorted segment of the list progresses.

• Best Case: O(n2)
• Worst Case: O(n2)
• Time Complexity Analysis: The worst case, average case, and best case time complexity of sorting algorithm Selection Sort is O(n2) because it always needs to look over the unsorted section of the array even if it is sorted initially. The algorithm is, generally speaking, slower than other more complex algorithms and is more frequently applied to small sets of data.

✅Insertion Sort

Insertion sort constructs a sorted list from left to right adding additional elements to the sorted portion of the list.

• Best Case: 𝑂(𝑛) — When the array is already sorted.
• Worst Case: O(n2) —  This occurs when the array is sorted in reverse
• Time Complexity Analysis: As mentioned before, Insertion Sort is highly efficient for handling small, or partially sorted, lists or arrays. It is particularly useful for small data sets because of its adaptive nature although it is not well applicable where large data sets are involved.

✅Merge Sort

Merge sort is a divide-and-conquer algorithm that sorts the given list in an efficient way by dividing them into two equal halves, then sorting the two halves individually, and then merging them.

• Best Case: O(nlogn)
• Worst Case: O(nlogn)
• Time Complexity Analysis: The time complexity of sorting algorithm Merge Sort in all cases is O(n log n), which is optimal for large data sets. This approach has stable sorting and maintains this stability in its performance but might need extra memory for the merge.

✅Quick Sort

Quick Sort also comes under the category of divide and conquer. This algorithm chooses an element called the ‘pivot’ and divides the array based on this element.

• Best Case: O(nlogn) — If the array or list is divided from the middle, that is, if n/2 elements smaller than the pivot are there and n/2 elements equal to the pivot are there.
• Worst Case: O(n2)
• Time Complexity Analysis: In contrast with Quick Sort we can say that Merge Sort usually takes more time as it uses the concept of in-place sorting. It means for large datasets, the pivot selection is very efficient.

✅Heap Sort

Heap Sort uses a binary heap data structure in its operation. It forms a max-heap and again and again, it extracts the largest element to place at the end of the array.

Best Case: O(nlogn)

Worst Case: O(nlogn)

Time Complexity Analysis: Heap Sort keeps a best and worst-case time complexity of O(nlogn) across cases and sorts in place and therefore is effective on large data sets. While average performance is worse than Quick Sort, in practice they are faster and better when you do not need to meet the stability requirement and have to meet the worst-case problem.

Comparative Analysis of Sorting Algorithms Time Complexity

This section presents a comparison of the commonly used sorting algorithms as a way of obtaining an understanding and evaluation of their performance. In this way, we can see a comparison for different cases called best, average, and worst time complexities.

Conclusion

There is no general sorting algorithm that can be opted for without first considering the size of the data, the system, and what performance is wanted. While for small data sets it is enough to use simple algorithms such as Insertion Sort, for large data sets, such as Merge Sort or Quick Sort are used most often.

In conclusion, it will be possible to decide on the characteristics of the data, as well as on the system’s requirements that will allow achieving the maximum efficiency of sorting.

Wishing you all the best — Happy coding! 🚀